预处理
预处理,即在正式处理数据之前的操作,通常目的是优化时间、空间复杂度。
前置知识:
- C++基础语法
本节目录:
前缀和与差分
二维前缀和与二维差分
离散化
总结
前缀和与差分
前缀和
我们先看例题:洛谷B3612 求区间和
简而言之,给你一个长度为$n$的正整数数组 $a_1,a_2,⋯,a_n$,有$m$次询问,每次询问给出一对区间$[ l_i, r_i ]$,分别求这 $m$ 个区间的区间和。
如果你不会前缀和算法,你可能会这样写……
#include <bits/stdc++.h>
using namespace std;
int arr[100005]; // 正整数数组
int main() {
int n; cin >> n; // 输入n
for(int i = 1; i <= n; ++ i) cin >> arr[i]; // 输入数据
int m; cin >> m; // 输入 m
int l, r;
for(int i = 1; i <= m; ++ i) {
int ans = 0; // 存结果
cin >> l >> r; // 输入l, r
for(int j = l; j <= r; ++ j) // 从l到r累加数组数据
ans += arr[j];
cout << ans << endl; // 输出ans
}
return 0;
}但是一提交,结果却……
TLE。 。 。
为什么会超时呢?我们研究一下时间复杂度。
按照最坏情况,$n = 10^5$,区间可能的最大范围是整个数组,也就是$[0, 10^5]$,内外层循环都是$n$次,所以$O(n^2)$的复杂度,循环次数为$10^{10}$,题目时间限制为$1s$,肯定会超时(只要出题人想卡你,显然这道题卡了)。(具体时间复杂度计算和运行时间,看我这篇博客:pass)
我们想一想,如果询问次数过多,可能会有重叠的区间被重复计算,也就造成,同一段数,不断被求和,导致性能的浪费。有没有一种方法,可以使每一个数只被计算一次,之后只需直接使用即可呢?
有的,那就是前缀和!
如果我们开辟一个额外的数组,前缀和数组(prefix,当然你取什么变量都行,只是为了显而易见得知道这个数组的作用),用来存储,原数组前$i$项的和,就是:
$$prefix[k] = \sum_{i=1}^k arr[i], (k = 1,2,…,n)$$
说人话就是:
$$prefix[k] = arr[1] + arr[2] + … + arr[k], (k = 1,2,…,n)$$
如果原数组$arr = [1, 2, 3, 4, 5]$
则:
$prefix[0] = 0$
$prefix[1] = arr[1] = 1$
$prefix[2] = arr[1] + arr[2] = 3$
$prefix[3] = arr[1] + arr[2] + arr[3] = 6$
$prefix[4] = arr[1] + arr[2] + arr[3] + arr[4] = 10$
$prefix[5] = arr[1] + arr[2] + arr[3] + arr[4] + arr[5]= 15$
观察可以得到:
$prefix[1] = prefix[0] + arr[1]$
$prefix[2] = prefix[1] + arr[2]$
$prefix[3] = prefix[2] + arr[3]$
$prefix[4] = prefix[3] + arr[4]$
$prefix[5] = prefix[4] + arr[5]$
预处理每项$prefix$:
对于每个$prefix[k]$,有递推式:
$$\boxed{prefix[k] = prefix[k - 1] + arr[k], (k = 1,2,…,n)}$$
注意到(注意力惊人),对于任意的$[l, r]$区间和$ans$就是:
$$\boxed{ans = \sum_{i=l}^r arr[i] = prefix[r] - prefix[l - 1]}$$
有了这两个式子,代码就很好写了:
#include <bits/stdc++.h>
using namespace std;
int arr[100005]; // 数组
int prefix[100005]; // 前缀和数组
int main() {
int n; cin >> n; // 输入n
for(int i = 1; i <= n; ++ i) { // 因为后面要i-1,所以从1开始,避免数组越界
cin >> arr[i]; // 输入数据
prefix[i] = prefix[i - 1] + arr[i]; // 预处理前缀和数组
}
int m; cin >> m; // 输入 m
int l, r;
for(int i = 1; i <= m; ++ i) {
cin >> l >> r; // 输入l, r
cout << prefix[r] - prefix[l - 1] << endl; // 直接计算得出答案
}
return 0;
}然后就愉快的AC啦!
时间复杂度$O(n)$(没有循环嵌套),空间复杂度也是$O(n)$.
因为$arr$数组之后不会再用到,所以可以再优化空间:
#include <bits/stdc++.h>
using namespace std;
// int arr[100005]; 直接不需要原数组
int prefix[100005]; // 前缀和数组
int main() {
int n; cin >> n; // 输入n
int num; // 临时变量num
for(int i = 1; i <= n; ++ i) {
cin >> num;
prefix[i] = prefix[i - 1] + num; //预处理前缀和数组
}
int m; cin >> m; // 输入 m
int l, r;
for(int i = 1; i <= m; ++ i) {
cin >> l >> r; // 输入l, r
cout << prefix[r] - prefix[l - 1] << endl; // 直接计算得出答案
}
return 0;
}以上,我们称$prefix$数组为前缀和数组,求取$prefix$数组的过程为前缀和算法。
前缀和算法可以简化频繁的区间求和操作,但局限是只能离线操作,就是说,如果涉及对数组的值进行更改的操作,就无法使用前缀和。
差分
还是先看例题:洛谷P2367 语文成绩
简而言之:给你一个长度为 $n$ 的数组,给定 $p$ 次操作,每次操作给你三个数 $x, y, z$ ,意为:给第 $x$ 个数到第 $y$ 个数每个数增加 $z$ 。最后输出操作完数组中的最小值。
若初始数组为 nums = [1, 1, 1, 1, 1]
一次为操作:1 2 1
结果为: nums = [2, 2, 1, 1, 1]
第二次操作为:2 4 2
结果为: nums = [2, 4, 3, 3, 1]
如果你还是只会暴力。。
不用想一定会超时,因为 $n <= 5e6$,纯暴力时间复杂度为$O(n^2)$, 明显超出了$1e9$。
如果你不信邪,可以暴力尝试一下:)
这题我们需要使用差分。
我们使用一个数组记录数据之间的差值,这个数组我们称为$diff$数组,和前缀和数组一样,也需要我们预处理出来。
对于数组$nums$:
$$diff[i] = nums[i] - nums[i - 1]$$
我们发现,对于$diff$数组做一次前缀和,可以得到原数组。
$$nums[i] = \sum_{j = 1}^i diff[j]$$
这个证明可以自行百度。
差分是前缀和的逆运算,反之亦然
对于差分数组,有一个很好的性质:
假如要对原数组区间 $[l, r]$ 都加上 $z$,只需在$diff[l]$加上$z$,$diff[r + 1]$ 减去 $z$。
即:diff[l] += zdiff[r + 1] -= z
因为diff数组是数据之间的差,对于一个区间加上一个数,这个区间之间的数的差值不会改变,因为都变化了,只有端点处有改变,所以只需改变端点处的值即可。
我们对$diff$数组不断进行此操作,最后,通过一次前缀和操作,得到原数组,顺便找到最小值,代码如下:
#include <bits/stdc++.h>
using namespace std;
int diff[5000005]; // 差分数组
int nums[5000005]; // 原数组
int main() {
int n, p; cin >> n >> p;
for(int i = 1; i <= n; ++ i) {
cin >> nums[i]; // 输入原数组
}
for(int i = 1; i <= n; ++ i) {
diff[i] = nums[i] - nums[i - 1]; // 计算差分数组
}
while(p --) { // p 次查询
int x, y, z;
cin >> x >> y >> z;
diff[x] += z; // 计算累加
diff[y + 1] -= z;
}
int ans = INT_MAX; // int的最大值,用于找到最小值
int num = 0;
for(int i = 1; i <= n; ++ i) {
num += diff[i]; // 前缀和操作
ans = min(ans, num); // 顺便找到最小值
}
cout << ans << "\n";
return 0;
}然后就AC啦!
二维前缀和与二维差分
二维前缀和
先看例题:P2004 领地选择
简单来说:给定一个 $N \times M$ 的数字地图,选择一个 $C \times C$ 的一个小正方形,要使得这个正方形内的数之和最大,输出这个正方形左上角的坐标。
这是一个二维前缀和的模板题。
我们需要先求出对于坐标原点的所有矩形之中的数之和。
我们创建一个二维$prefix$数组,用于存取每个点到原点之间的矩形的数字和。
例如坐标 $(a, b)$ 存取的数字为如图区域的和。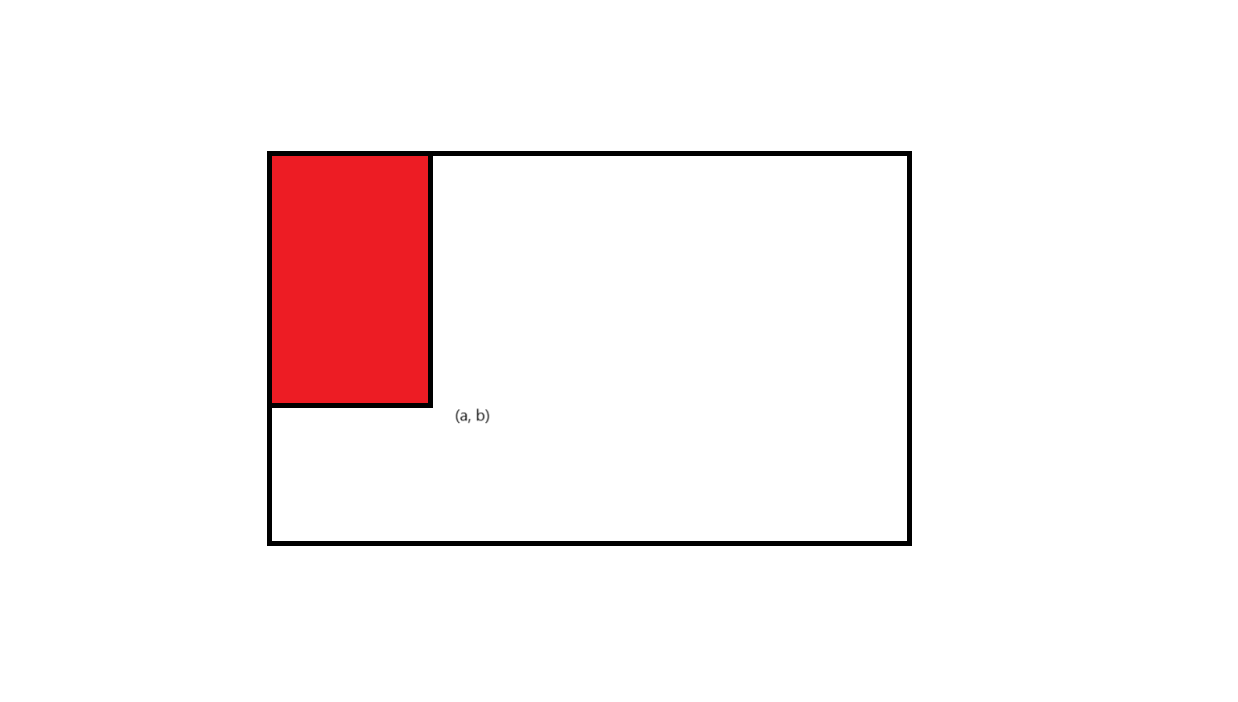
如果对于原数组为: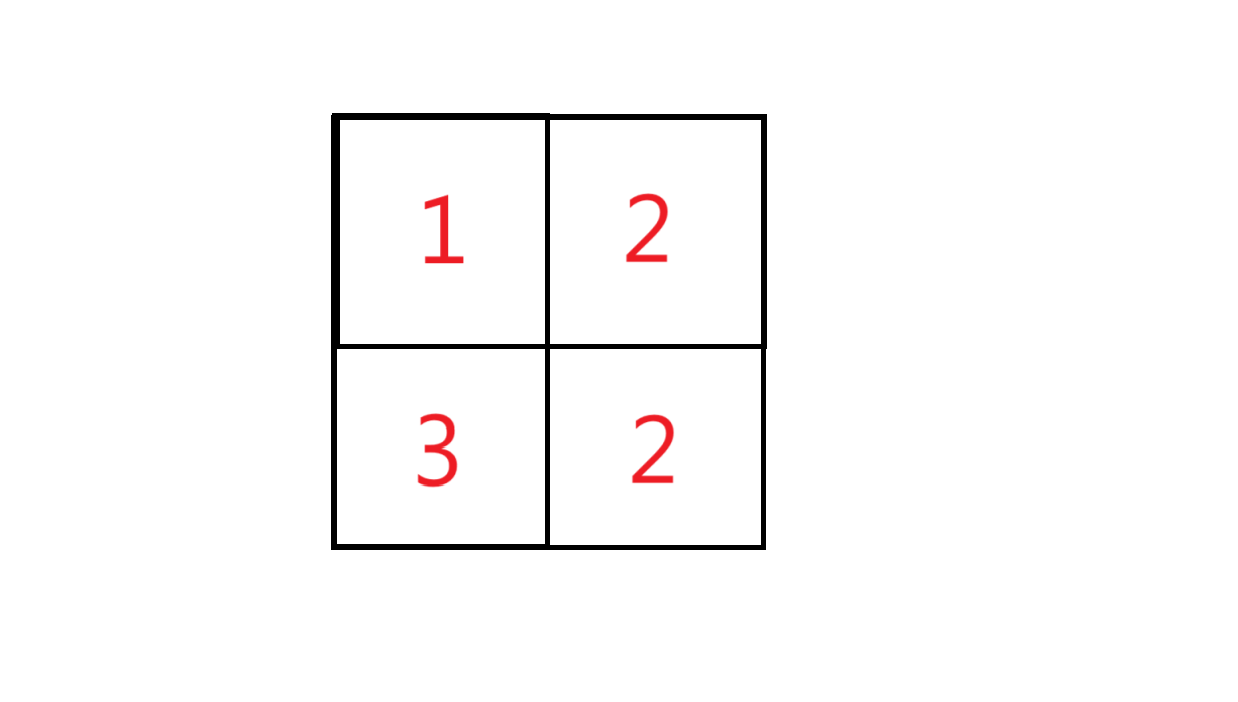
$prefix$数组为: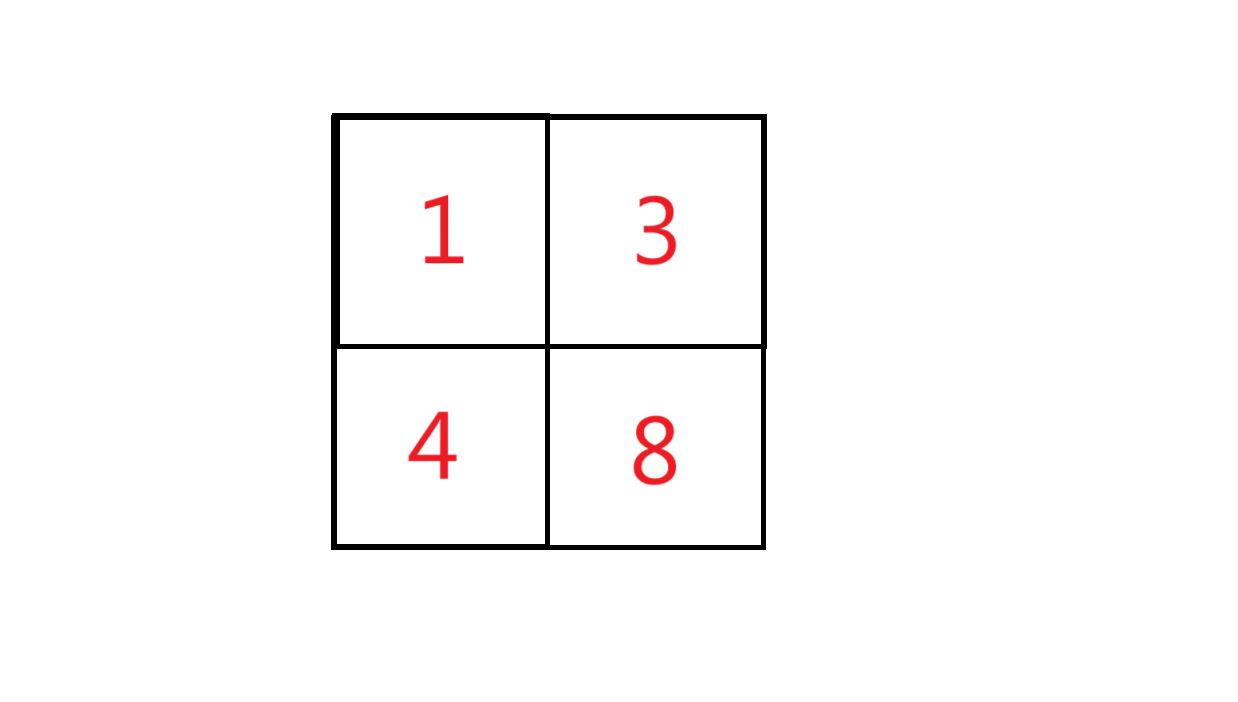
不难发现,由于容斥原理,每一项 $prefix[i][j]$ 的值为:
$$prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + nums[i][j]$$
每一项的值为,它左边的值: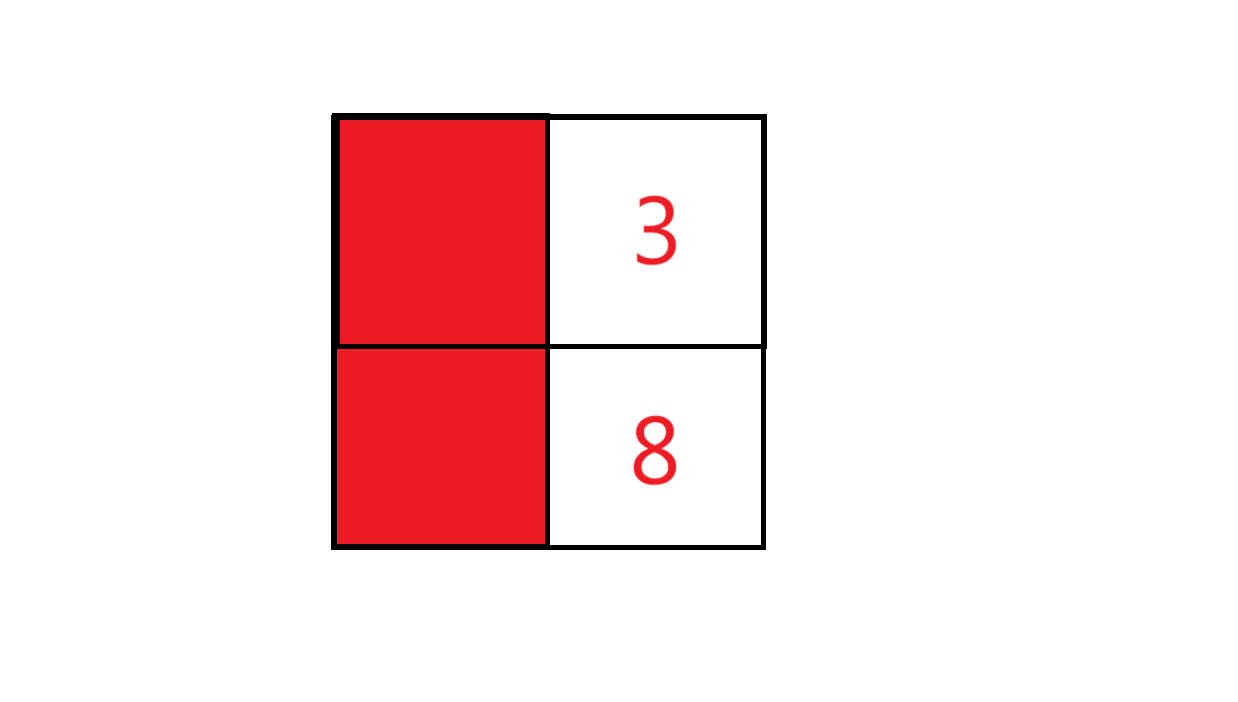
加上它上面的值: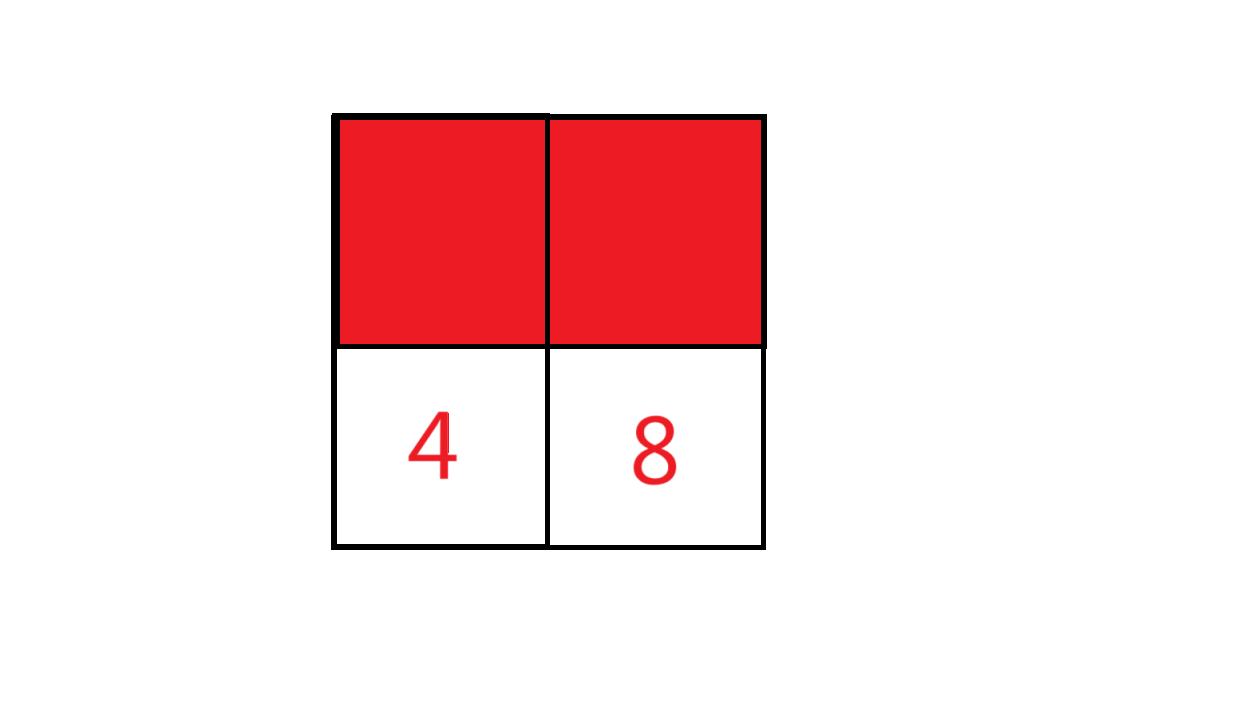
减去左上重复加过的一个: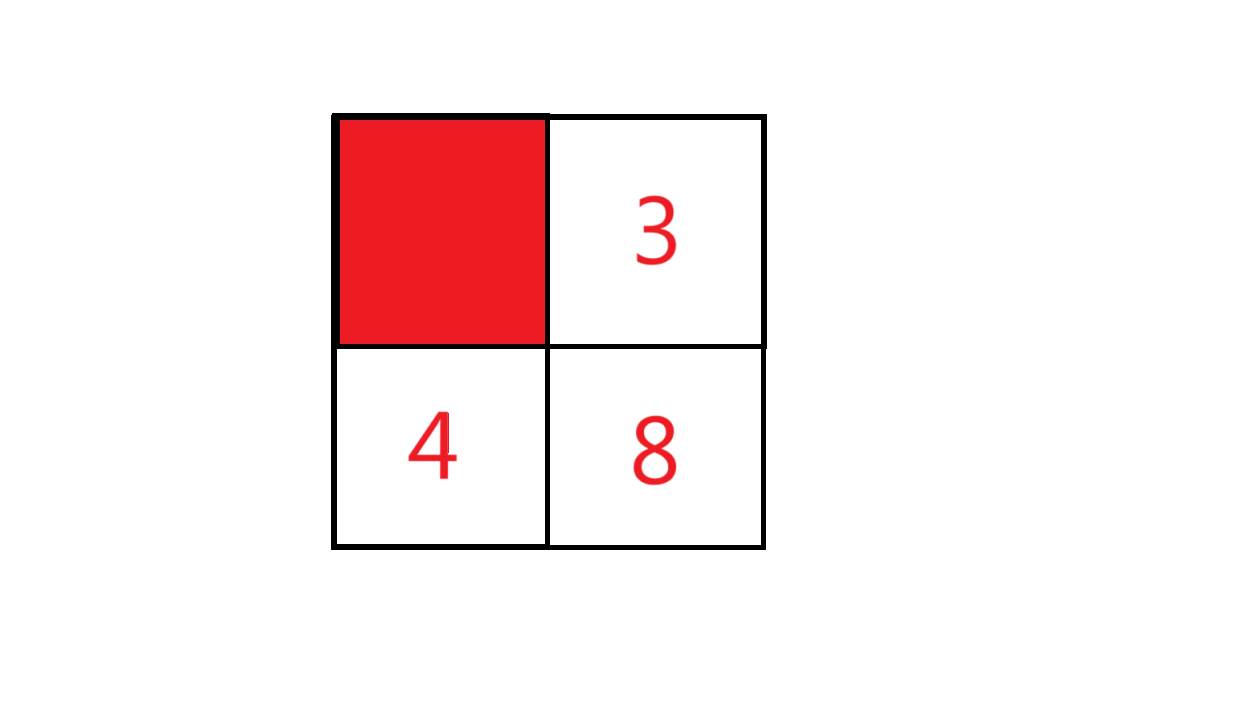
再加上本身: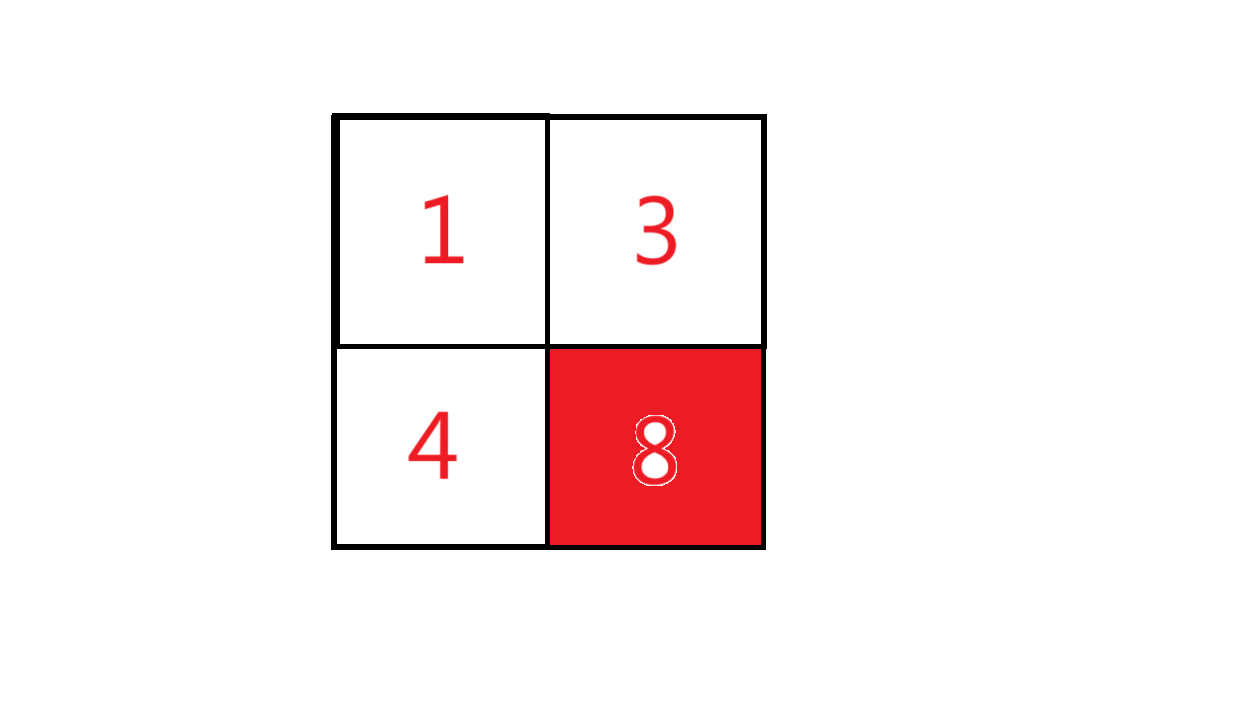
所以对于$(C, C)$开始,每个$C \times C$ 等于:
$$ans = prefix[i][j] - prefix[i - C][j] - prefix[i][j - C] + prefix[i - C][j - C]$$
同理:当前区域减去左边减去右边,加上右上角多减去的一次。
AC Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long; // long long的简写
ll prefix[1005][1005]; // 差分数组,可能会爆int,需要long long
int main() {
int N, M, C;
cin >> N >> M >> C;
int num = 0;
for(int i = 1; i <= N; ++ i) {
for(int j = 1; j <= M; ++ j) {
cin >> num;
prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + num;
// 处理二维前缀和
}
}
ll ans = 0; // 同样可能爆int
int x = 0, y = 0;
for(int i = C; i <= N; ++ i) {
for(int j = C; j <= M; ++ j) {
ll res = prefix[i][j] - prefix[i - C][j] - prefix[i][j - C] + prefix[i - C][j - C];
if(res > ans) {
ans = res; // 计算最大值
x = i - C + 1; // 记录坐标
y = j - C + 1;
}
}
}
cout << x << " " << y << "\n"; // 输出坐标
return 0;
}二维差分
例题:洛谷P3397 地毯
在 $n \times n$ 的格子上有 $m$ 个地毯,给你 $m$ 次操作,每次操作给你四个数 $x_1, y_1, x_2, y_2$,表示在左上角 $(x_1, y_1)$ 到右下角 $(x_2, y_2)$ 的区域上铺一个地毯。输出 $n$ 行,每行 $n $ 个正整数。第 $i$ 行第 $j$ 列的正整数表示 $(i,j)$ 这个格子被多少个地毯覆盖。
我们直接对原数组二维差分:
$$diff[i][j] = nums[i][j] - nums[i - 1][j] - nums[i][j - 1] + nums[i - 1][j - 1]$$
由于此题特殊,初始数组全都为 $0$,所以我们可以不需要进行二维差分,直接在原数组上操作即可。
对于每次操作,我们只需要在差分数组上进行如下操作:
diff[x1][y1] ++;
diff[x2 + 1][y2 + 1] ++;
diff[x1][y2 + 1] --;
diff[x2 + 1][y1] --;AC Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long; // long long的简写
int nums[1005][1005]; // 原数组
int main() {
int n, m;
cin >> n >> m;
while(m --) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
nums[x1][y1] ++; // 直接在原数组上操作
nums[x2 + 1][y2 + 1] ++;
nums[x1][y2 + 1] --;
nums[x2 + 1][y1] --;
}
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
nums[i][j] += nums[i - 1][j] + nums[i][j - 1] - nums[i - 1][j - 1]; // 二维前缀和
cout << nums[i][j] << " "; // 输出
}
cout << "\n";
}
return 0;
}离散化
离散化是将一个连续的数列映射到一个离散的数列上,通常用于处理区间问题。
离散化的思路是:将原数组中的数进行排序,去重,得到一个新的数组,然后用原数组中的数去映射新的数组,得到一个新的离散化后的数组。
离散化的步骤:
- 将原数组中的数进行排序,去重,得到一个新的数组。
- 用原数组中的数去映射新的数组,得到一个新的离散化后的数组。
- 对新的离散化后的数组进行处理,得到结果。
- 输出结果。
#include <bits/stdc++.h>
using namespace std;
using ll = long long; // long long的简写
int arr[100005]; // 原数组
int arr2[100005]; // 离散化后的数组
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; ++ i) {
cin >> arr[i]; // 输入原数组
arr2[i] = arr[i]; // 离散化后的数组
}
sort(arr2 + 1, arr2 + n + 1); // 排序
int len = unique(arr2 + 1, arr2 + n + 1) - arr2 - 1; // 去重
for(int i = 1; i <= n; ++ i) {
arr3[i] = lower_bound(arr2 + 1, arr2 + len + 1, arr[i]) - arr2; // 映射
cout << arr3[i] << " "; // 输出离散化后的数组
}
cout << "\n";
return 0;
}离散化的时间复杂度为 $O(n \log n)$,空间复杂度为 $O(n)$。
总结
预处理算法是一个非常重要的算法思想,能够有效地提高程序的运行效率。前缀和和差分是最常用的预处理算法,能够快速地计算区间和。二维前缀和和二维差分则是对前缀和和差分的扩展,能够处理二维数组的问题。离散化则是将连续的数列映射到离散的数列上,能够有效地处理区间问题。
预处理算法的应用非常广泛,尤其是在ACM竞赛中,掌握预处理算法的思想和技巧,对于提高解题效率和能力有很大的帮助。
完结撒花!!!

